Introducing: the ambition-to-competence ratio in kleptocracies
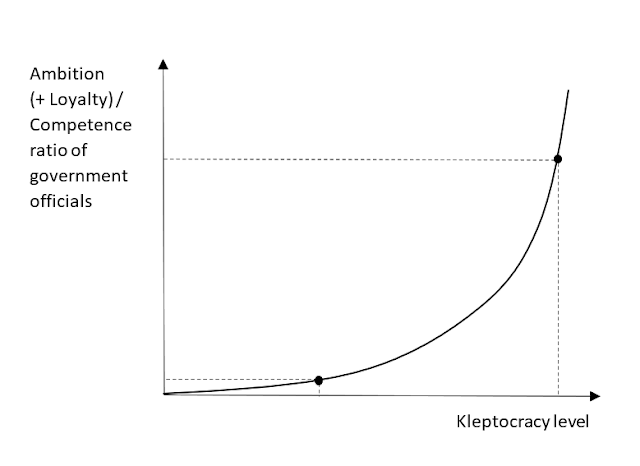
Russia's invasion of Ukraine has inspired me to come up with an interesting theoretical concept. I'll lay it out first, and then try to explain the reasoning behind it and how it can be used to explain potential outcomes of Russia's Ukraine invasion. The ambition-to-competence ratio of government officials is an exponential function of the kleptocracy level of a country. It is best defined as ambition plus loyalty divided by one’s intrinsic level of competence: A-C ratio = (ambition + loyalty ) / intrinsic competence In high-level kleptocracies, where the government is completely subdued to a ruling elite looking to expropriate wealth of the country they govern (e.g. the dictator and his cronies, oligarchs, or the military), government officials rise in rank based on their ambition and their loyalty. Their competence is inversely related to their rank in government. This means that in kleptocracies it is possible (and even desirable) to move up the hierarchy purely bas



